User-User Collaborative Filtering Using Neo4j Graph Database
Sun, Nov 5, 2017Motivation ¶
Recommendation systems fall under two categories: personalized and non-personalized recommenders. My previous post on association rules mining is an example of a non-personalized recommender, as the recommendations generated are not tailored to a specific user. By contrast, a personalized recommender system takes into account user preferences in order to make recommendations for that user. There are various personalized recommender algorithms, and in this post, I will be implementing user-user collaborative filtering. This algorithm finds users similar to the target user in order to generate recommendations for the target user. And to add to the fun, I will be implementing the algorithm using a graph database versus the more traditional approach of matrix factorization.
User-User Collaborative Filtering ¶
This personalized recommender algorithm assumes that past agreements predict future agreements. It uses the concept of similarity in order to identify users that are "like" the target user in terms of their preferences. Users identified as most similar to the target user become part of the target user's neighbourhood. Preferences of these neighbours are then used to generate recommendations for the target user.
Concretely, here are the steps we will be implementing to generate recommendations for an online grocer during the user check-out process:
- Select a similarity metric to quantify likeness between users in the system.
- For each user pair, compute similarity metric.
- For each target user, select the top k neighbours based on the similarity metric.
- Identify products purchased by the top k neighbours that have not been purchased by the target user.
- Rank these products by the number of purchasing neighbours.
- Recommend the top n products to the target user.
In this particular demonstration, we are building a recommender system based on the preferences of 100 users. As such, we would like the neighbourhood size, k, to be large enough to identify clear agreement between users, but not too large that we end up including those that are not very similar to the target user. Hence we choose k=10. Secondly, in the context of a user check-out application for an online grocer, the goal is to increase user basket by surfacing products that are as relevant as possible, without overwhelming the user. Therefore we limit the number of recommendations to n=10 products per user.
Jaccard Index ¶
The Jaccard index measures similarity between two sets, with values ranging from 0 to 1. A value of 0 indicates that the two sets have no elements in common, while a value of 1 implies that the two sets are identical. Given two sets A and B, the Jaccard index is computed as follows:
$$J(A,B) = \frac{| A \cap B |} {| A \cup B |}$$The numerator is the number of elements that A and B have in common, while the denominator is the number of elements that are unique to each set.
In this implementation of user-user collaborative filtering, we will be using the Jaccard index to measure similarity between two users. This is primarily due to the sparse nature of the data, where there is a large number of products and each user purchases only a small fraction of those products. If we were to model our user preferences using binary attributes (ie: 1 if user purchased product X and 0 if user did not purchase product X), we would have a lot of 0s and very few 1s. The Jaccard index is effective in this case, as it eliminates matching attributes that have a value of 0 for both users. In other words, when computing similarity between two users, we only consider products that have been purchased, either by both users, or at least one of the users. Another great thing about the Jaccard index is that it accounts for cases where one user purchases significantly more products than the user it's being compared to. This can result in higher overlap of products purchased between the two, but this does not necessarily mean that the two users are similar. With the equation above, we see that the denominator will be large, thereby resulting in a smaller Jaccard index value.
Graph Database ¶
A graph database is a way of representing and storing data. Unlike a relational database which represents data as rows and columns, data in a graph database is represented using nodes, edges and properties. This representation makes graph databases conducive to storing data that is inherently connected. For our implementation of user-user collaborative filtering, we are interested in the relationships that exist between users based on their preferences. In particular, we have a system comprised of users who ordered orders, and these orders contain products that are in a department and in an aisle. These relationships are easily depicted using a property graph data model:
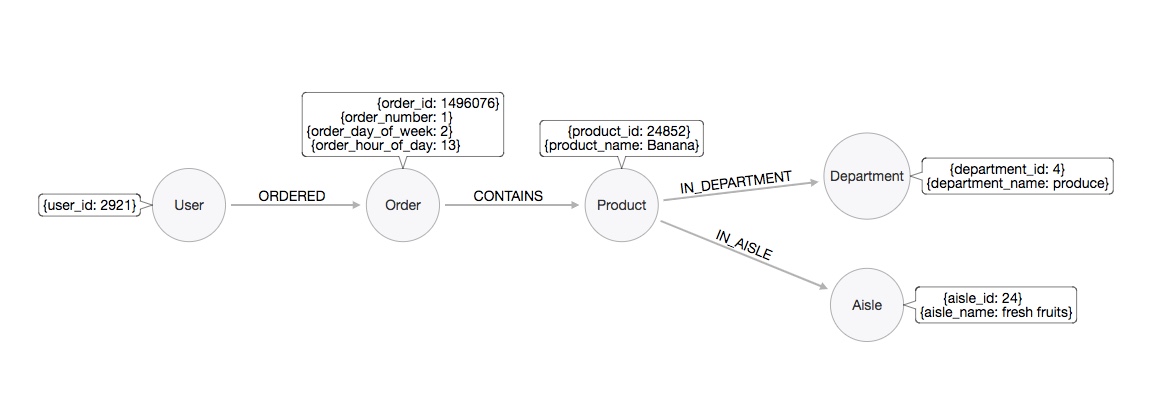
The nodes represent entities in our system: User, Order, Product, Department and Aisle. The edges represent relationships: ORDERED, CONTAINS, IN_DEPARTMENT and IN_AISLE. The attributes in the nodes represent properties (eg: a User has property "user_id"). Mapping to natural language, we can generally think of nodes as nouns, edges as verbs and properties as adjectives.
In this particular graph, each node type contains the same set of properties (eg: all Orders have an order_id, order_number, order_day_of_week and order_hour_of_day), but one of the interesting properties of graph databases is that it is schema-free. This means that a node can have an arbitrary set of properties. For example, we can have two user nodes, u1 and u2, with u1 having properties such as name, address and phone number, and u2 having properties such as name and email. The concept of a schema-free model also applies to the relationships that exist in the graph.
We will be implementing the property graph model above using Neo4j, arguably the most popular graph database today. The actual creation and querying of the database will be done using the Cypher query language, often thought of as SQL for graphs.
Input Dataset ¶
Similar to my post on association rules mining, we will once again be using data from Instacart. The datasets can be downloaded from the link below, along with the data dictionary:
“The Instacart Online Grocery Shopping Dataset 2017”, Accessed from https://www.instacart.com/datasets/grocery-shopping-2017 on Oct 10, 2017.
Part 1: Data Preparation ¶
import pandas as pd
import numpy as np
import sys
# Utility functions
# Returns the size of an object in MB
def size(obj):
return "{0:.2f} MB".format(sys.getsizeof(obj) / (1000 * 1000))
# Displays dataframe dimensions, size and top 5 records
def inspect_df(df_name, df):
print('{0} --- dimensions: {1}; size: {2}'.format(df_name, df.shape, size(df)))
display(df.head())
# Exports dataframe to CSV, the format for loading data into Neo4j
def export_to_csv(df, out):
df.to_csv(out, sep='|', columns=df.columns, index=False)
A. Load user order data ¶
Data from Instacart contains 3-99 orders per user. Inspecting the distribution of number of orders per user, we see that users place 16 orders on average, with 75% of the user base placing at least 5 orders. For demonstration purposes, we will be running collaborative filtering on a random sample of 100 users who purchased at least 5 orders.
min_orders = 5 # minimum order count per user
sample_count = 100 # number of users to select randomly
# Load data from evaluation set "prior" (please see data dictionary for definition of 'eval_set')
order_user = pd.read_csv('orders.csv')
order_user = order_user[order_user['eval_set'] == 'prior']
# Get distribution of number of orders per user
user_order_count = order_user.groupby('user_id').agg({'order_id':'count'}).rename(columns={'order_id':'num_orders'}).reset_index()
print('Distribution of number of orders per user:')
display(user_order_count['num_orders'].describe())
# Select users who purchased at least 'min_orders'
user_order_atleast_x = user_order_count[user_order_count['num_orders'] >= min_orders]
# For reproducibility, set seed before taking a random sample
np.random.seed(1111)
user_sample = np.random.choice(user_order_atleast_x['user_id'], sample_count, replace=False)
# Subset 'order_user' to include records associated with the 100 randomly selected users
order_user = order_user[order_user['user_id'].isin(user_sample)]
order_user = order_user[['order_id','user_id','order_number','order_dow','order_hour_of_day']]
inspect_df('order_user', order_user)
B. Load order details data ¶
# Load orders associated with our 100 selected users, along with the products contained in those orders
order_product = pd.read_csv('order_products__prior.csv')
order_product = order_product[order_product['order_id'].isin(order_user.order_id.unique())][['order_id','product_id']]
inspect_df('order_product', order_product)
C. Load product data ¶
# Load products purchased by our 100 selected users
products = pd.read_csv('products.csv')
products = products[products['product_id'].isin(order_product.product_id.unique())]
inspect_df('products', products)
D. Load aisle data ¶
# Load entire aisle data as it contains the names related to the aisle IDs from the 'products' data
aisles = pd.read_csv('aisles.csv')
inspect_df('aisles', aisles)
E. Load department data ¶
# Load entire department data as it contains the names related to the department IDs from the 'products' data
departments = pd.read_csv('departments.csv')
inspect_df('departments', departments)
F. Export dataframes to CSV, which in turn will be loaded into Neo4j ¶
export_to_csv(order_user, '~/neo4j_instacart/import/neo4j_order_user.csv')
export_to_csv(order_product, '~/neo4j_instacart/import/neo4j_order_product.csv')
export_to_csv(products, '~/neo4j_instacart/import/neo4j_products.csv')
export_to_csv(aisles, '~/neo4j_instacart/import/neo4j_aisles.csv')
export_to_csv(departments, '~/neo4j_instacart/import/neo4j_departments.csv')
Part 2: Create Neo4j Graph Database ¶
A. Set up authentication and connection to Neo4j ¶
# py2neo allows us to work with Neo4j from within Python
from py2neo import authenticate, Graph
# Set up authentication parameters
authenticate("localhost:7474", "neo4j", "xxxxxxxx")
# Connect to authenticated graph database
g = Graph("http://localhost:7474/db/data/")
B. Start with an empty database, then create constraints to ensure uniqueness of nodes ¶
# Each time this notebook is run, we start with an empty graph database
g.run("MATCH (n) DETACH DELETE n;")
# We drop and recreate our node constraints
g.run("DROP CONSTRAINT ON (order:Order) ASSERT order.order_id IS UNIQUE;")
g.run("DROP CONSTRAINT ON (user:User) ASSERT user.user_id IS UNIQUE;")
g.run("DROP CONSTRAINT ON (product:Product) ASSERT product.product_id IS UNIQUE;")
g.run("DROP CONSTRAINT ON (aisle:Aisle) ASSERT aisle.aisle_id IS UNIQUE;")
g.run("DROP CONSTRAINT ON (department:Department) ASSERT department.department_id IS UNIQUE;")
g.run("CREATE CONSTRAINT ON (order:Order) ASSERT order.order_id IS UNIQUE;")
g.run("CREATE CONSTRAINT ON (user:User) ASSERT user.user_id IS UNIQUE;")
g.run("CREATE CONSTRAINT ON (product:Product) ASSERT product.product_id IS UNIQUE;")
g.run("CREATE CONSTRAINT ON (aisle:Aisle) ASSERT aisle.aisle_id IS UNIQUE;")
g.run("CREATE CONSTRAINT ON (department:Department) ASSERT department.department_id IS UNIQUE;")
C. Load product data into Neo4j ¶
query = """
// Load and commit every 500 records
USING PERIODIC COMMIT 500
LOAD CSV WITH HEADERS FROM 'file:///neo4j_products.csv' AS line FIELDTERMINATOR '|'
WITH line
// Create Product, Aisle and Department nodes
CREATE (product:Product {product_id: toInteger(line.product_id), product_name: line.product_name})
MERGE (aisle:Aisle {aisle_id: toInteger(line.aisle_id)})
MERGE (department:Department {department_id: toInteger(line.department_id)})
// Create relationships between products and aisles & products and departments
CREATE (product)-[:IN_AISLE]->(aisle)
CREATE (product)-[:IN_DEPARTMENT]->(department);
"""
g.run(query)
D. Load aisle data into Neo4j ¶
query = """
// Aisle data is very small, so there is no need to do periodic commits
LOAD CSV WITH HEADERS FROM 'file:///neo4j_aisles.csv' AS line FIELDTERMINATOR '|'
WITH line
// For each Aisle node, set property 'aisle_name'
MATCH (aisle:Aisle {aisle_id: toInteger(line.aisle_id)})
SET aisle.aisle_name = line.aisle;
"""
g.run(query)
E. Load department data into Neo4j ¶
query = """
// Department data is very small, so there is no need to do periodic commits
LOAD CSV WITH HEADERS FROM 'file:///neo4j_departments.csv' AS line FIELDTERMINATOR '|'
WITH line
// For each Department node, set property 'department_name'
MATCH (department:Department {department_id: toInteger(line.department_id)})
SET department.department_name = line.department;
"""
g.run(query)
F. Load order details data into Neo4j ¶
query = """
// Load and commit every 500 records
USING PERIODIC COMMIT 500
LOAD CSV WITH HEADERS FROM 'file:///neo4j_order_product.csv' AS line FIELDTERMINATOR '|'
WITH line
// Create Order nodes and then create relationships between orders and products
MERGE (order:Order {order_id: toInteger(line.order_id)})
MERGE (product:Product {product_id: toInteger(line.product_id)})
CREATE (order)-[:CONTAINS]->(product);
"""
g.run(query)
G. Load user order data into Neo4j ¶
query = """
// Load and commit every 500 records
USING PERIODIC COMMIT 500
LOAD CSV WITH HEADERS FROM 'file:///neo4j_order_user.csv' AS line FIELDTERMINATOR '|'
WITH line
// Create User nodes and then create relationships between users and orders
MERGE (order:Order {order_id: toInteger(line.order_id)})
MERGE (user:User {user_id: toInteger(line.user_id)})
// Create relationships between users and orders, then set Order properties
CREATE(user)-[o:ORDERED]->(order)
SET order.order_number = toInteger(line.order_number),
order.order_day_of_week = toInteger(line.order_dow),
order.order_hour_of_day = toInteger(line.order_hour_of_day);
"""
g.run(query)
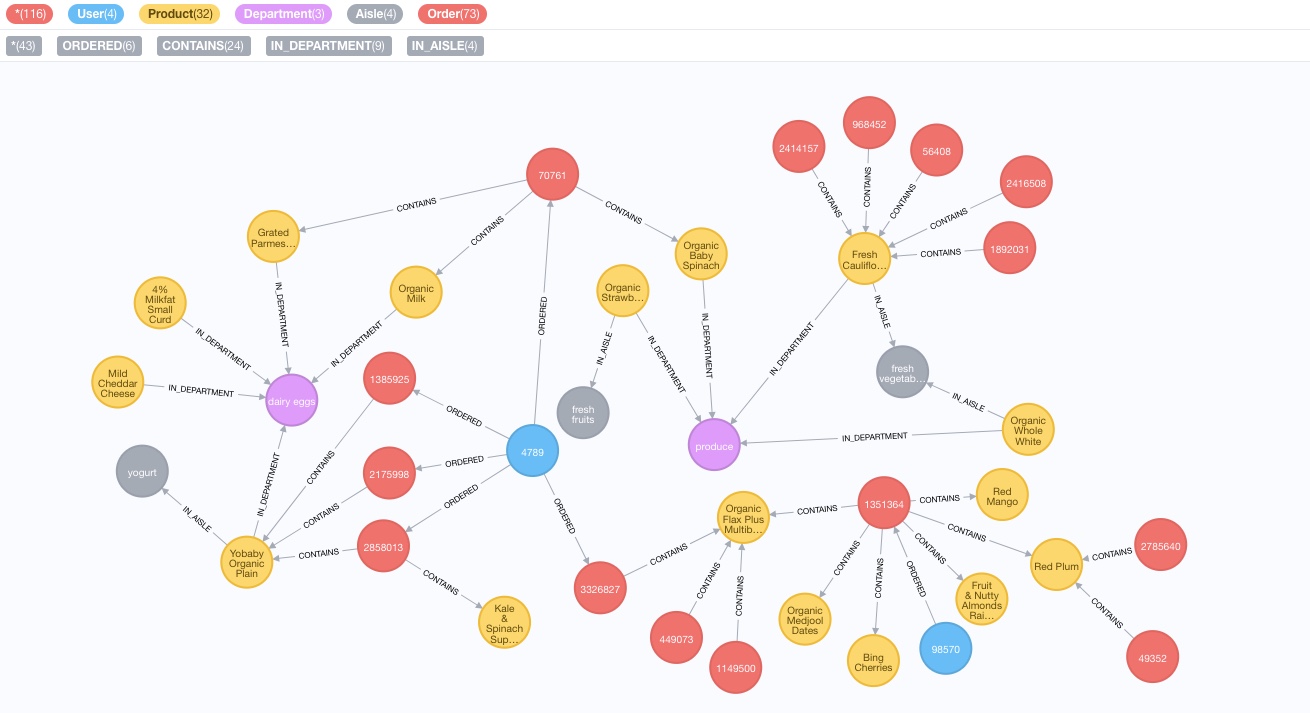
H. What our graph looks like ¶
This is what the nodes and relationships we have created look like in Neo4j for a small subset of the data. Please use the legend on the top left corner only to determine the colours associated with the different nodes (ie: ignore the numbers).
Part 3: Implement User-User Collaborative Filtering Algorithm ¶
# Implements user-user collaborative filtering using the following steps:
# 1. For each user pair, compute Jaccard index
# 2. For each target user, select top k neighbours based on Jaccard index
# 3. Identify products purchased by the top k neighbours that have not been purchased by the target user
# 4. Rank these products by the number of purchasing neighbours
# 5. Return the top n recommendations for each user
def collaborative_filtering(graph, neighbourhood_size, num_recos):
query = """
// Get user pairs and count of distinct products that they have both purchased
MATCH (u1:User)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product)<-[:CONTAINS]-(:Order)<-[:ORDERED]-(u2:User)
WHERE u1 <> u2
WITH u1, u2, COUNT(DISTINCT p) as intersection_count
// Get count of all the distinct products that they have purchased between them
MATCH (u:User)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product)
WHERE u in [u1, u2]
WITH u1, u2, intersection_count, COUNT(DISTINCT p) as union_count
// Compute Jaccard index
WITH u1, u2, intersection_count, union_count, (intersection_count*1.0/union_count) as jaccard_index
// Get top k neighbours based on Jaccard index
ORDER BY jaccard_index DESC, u2.user_id
WITH u1, COLLECT(u2)[0..{k}] as neighbours
WHERE LENGTH(neighbours) = {k} // only want users with enough neighbours
UNWIND neighbours as neighbour
WITH u1, neighbour
// Get top n recommendations from the selected neighbours
MATCH (neighbour)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product) // get all products bought by neighbour
WHERE not (u1)-[:ORDERED]->(:Order)-[:CONTAINS]->(p) // which target user has not already bought
WITH u1, p, COUNT(DISTINCT neighbour) as cnt // count neighbours who purchased product
ORDER BY u1.user_id, cnt DESC // sort by count desc
RETURN u1.user_id as user, COLLECT(p.product_name)[0..{n}] as recos // return top n products
"""
recos = {}
for row in graph.run(query, k=neighbourhood_size, n=num_recos):
recos[row[0]] = row[1]
return recos
Part 4: Execute User-User Collaborative Filtering ¶
Our collaborative filtering function expects 3 parameters: a graph database, the neighbourhood size and the number of products to recommend to each user. A reminder that our graph database, g, contains nodes and relationships pertaining to user orders. And as previously discussed, we have chosen k=10 as the neighbourhood size and n=10 as the number of products to recommend to each of our users. We now invoke our collaborative filtering function using these parameters.
%%time
recommendations = collaborative_filtering(g,10,10)
display(recommendations)
As can be seen above, our collaborative filtering function returns a dictionary of users and their top 10 recommended products. To see how we arrived at the output above, let's break down our function using a speficic example, user 4789. For reference, below are the products that this user has been recommended:
recommendations[4789]
The first main component of our collaborative filtering function identifies the top 10 neighbours for user 4789. It does so by creating user pairs, where u1 is always user 4789 and u2 is any other user who has purchased products that u1 has purchased. It then computes the Jaccard index for each user pair, by taking the number of distinct products that u1 and u2 have purchased in common (intersection_count) and dividing it by the number of distinct products that are unique to each user (union_count). The 10 users with the highest Jaccard index are selected as user 4789's neighbourhood.
query = """
// Get count of all distinct products that user 4789 has purchased and find other users who have purchased them
MATCH (u1:User)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product)<-[:CONTAINS]-(:Order)<-[:ORDERED]-(u2:User)
WHERE u1 <> u2
AND u1.user_id = {uid}
WITH u1, u2, COUNT(DISTINCT p) as intersection_count
// Get count of all the distinct products that are unique to each user
MATCH (u:User)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product)
WHERE u in [u1, u2]
WITH u1, u2, intersection_count, COUNT(DISTINCT p) as union_count
// Compute Jaccard index
WITH u1, u2, intersection_count, union_count, (intersection_count*1.0/union_count) as jaccard_index
// Get top k neighbours based on Jaccard index
ORDER BY jaccard_index DESC, u2.user_id
WITH u1, COLLECT([u2.user_id, jaccard_index, intersection_count, union_count])[0..{k}] as neighbours
WHERE LENGTH(neighbours) = {k} // only want to return users with enough neighbours
RETURN u1.user_id as user, neighbours
"""
neighbours = {}
for row in g.run(query, uid=4789, k=10):
neighbours[row[0]] = row[1]
print("Labels for user 4789's neighbour list: user_id, jaccard_index, intersection_count, union count")
display(neighbours)
The second main component of our collaborative filtering function generates recommendations for user 4789 using the neighbours identified above. It does so by considering products that the neighbours have purchased which user 4789 has not already purchased. The function then counts the number of neighbours who have purchased each of the candidate products. The 10 products with the highest neighbour count are selected as recommendations for user 4789.
%%time
query = """
// Get top n recommendations for user 4789 from the selected neighbours
MATCH (u1:User),
(neighbour:User)-[:ORDERED]->(:Order)-[:CONTAINS]->(p:Product) // get all products bought by neighbour
WHERE u1.user_id = {uid}
AND neighbour.user_id in {neighbours}
AND not (u1)-[:ORDERED]->(:Order)-[:CONTAINS]->(p) // which u1 has not already bought
WITH u1, p, COUNT(DISTINCT neighbour) as cnt // count times purchased by neighbours
ORDER BY u1.user_id, cnt DESC // and sort by count desc
RETURN u1.user_id as user, COLLECT([p.product_name,cnt])[0..{n}] as recos
"""
recos = {}
for row in g.run(query, uid=4789, neighbours=[42145,138203,87350,49441,187754,180461,120660,107931,73477,154852], n=10):
recos[row[0]] = row[1]
print("Labels for user 4789's recommendations list: product, number of purchasing neighbours")
display(recos)
Part 5: Evaluating Recommender Performance ¶
If we were to actually integrate our recommender system in to a production environment, we would need a way to measure its performance. As mentioned, in the context of a user check-out application for an online grocer, the goal is to increase basket size, by surfacing a short list of products that are as relevant as posssible to the user. For this particular application, we could choose precision as our metric for evaluating our recommender's performance. Precision is computed as the proportion of products that the user actually purchased, out of all the products that user has been recommended. To determine overall recommender performance, average precision can be calculated using the precision values for all the users in the system.
Conclusion ¶
We have demonstrated how to build a user-based recommender system leveraging the principles of user-user collaborative filtering. We've discussed the key concepts underlying this algorithm, from identifying neighbourhoods using a similarity metric, to generating recommendations for a user based on its neighbours' preferences. In addition, we have shown how easy and intuitive modeling connected data can be with a graph database. One final point worth noting: in real world applications, we may want to implement non-personalized recommendation strategies for users who are new to the system and those who have not yet made sufficient purchases. Strategies may include recommending top selling products for new users, and for the latter group, products identified to have high affinity with other products that the user has already purchased. This can be done through association rules mining, also known as market basket analysis.
Association Rules Mining Using Python Generators to Handle Large Datasets
Tue, Sep 12, 2017Motivation¶
I was looking to run association analysis in Python using the apriori algorithm to derive rules of the form {A} -> {B}. However, I quickly discovered that it's not part of the standard Python machine learning libraries. Although there are some implementations that exist, I could not find one capable of handling large datasets. "Large" in my case was an orders dataset with 32 million records, containing 3.2 million unique orders and about 50K unique items (file size just over 1 GB). So, I decided to write my own implementation, leveraging the apriori algorithm to generate simple {A} -> {B} association rules. Since I only care about understanding relationships between any given pair of items, using apriori to get to item sets of size 2 is sufficient. I went through various iterations, splitting the data into multiple subsets just so I could get functions like crosstab and combinations to run on my machine with 8 GB of memory. :) But even with this approach, I could only process about 1800 items before my kernel would crash... And that's when I learned about the wonderful world of Python generators.
Python Generators¶
In a nutshell, a generator is a special type of function that returns an iterable sequence of items. However, unlike regular functions which return all the values at once (eg: returning all the elements of a list), a generator yields one value at a time. To get the next value in the set, we must ask for it - either by explicitly calling the generator's built-in "next" method, or implicitly via a for loop. This is a great property of generators because it means that we don't have to store all of the values in memory at once. We can load and process one value at a time, discard when finished and move on to process the next value. This feature makes generators perfect for creating item pairs and counting their frequency of co-occurence. Here's a concrete example of what we're trying to accomplish:
-
Get all possible item pairs for a given order
eg: order 1: apple, egg, milk --> item pairs: {apple, egg}, {apple, milk}, {egg, milk} order 2: egg, milk --> item pairs: {egg, milk} -
Count the number of times each item pair appears
eg: {apple, egg}: 1 {apple, milk}: 1 {egg, milk}: 2
Here's the generator that implements the above tasks:
import numpy as np
from itertools import combinations, groupby
from collections import Counter
# Sample data
orders = np.array([[1,'apple'], [1,'egg'], [1,'milk'], [2,'egg'], [2,'milk']], dtype=object)
# Generator that yields item pairs, one at a time
def get_item_pairs(order_item):
# For each order, generate a list of items in that order
for order_id, order_object in groupby(orders, lambda x: x[0]):
item_list = [item[1] for item in order_object]
# For each item list, generate item pairs, one at a time
for item_pair in combinations(item_list, 2):
yield item_pair
# Counter iterates through the item pairs returned by our generator and keeps a tally of their occurrence
Counter(get_item_pairs(orders))
get_item_pairs() generates a list of items for each order and produces item pairs for that order, one pair at a time. The first item pair is passed to Counter which keeps track of the number of times an item pair occurs. The next item pair is taken, and again, passed to Counter. This process continues until there are no more item pairs left. With this approach, we end up not using much memory as item pairs are discarded after the count is updated.
Apriori Algorithm¶
Apriori is an algorithm used to identify frequent item sets (in our case, item pairs). It does so using a "bottom up" approach, first identifying individual items that satisfy a minimum occurence threshold. It then extends the item set, adding one item at a time and checking if the resulting item set still satisfies the specified threshold. The algorithm stops when there are no more items to add that meet the minimum occurrence requirement. Here's an example of apriori in action, assuming a minimum occurence threshold of 3:
order 1: apple, egg, milk
order 2: carrot, milk
order 3: apple, egg, carrot
order 4: apple, egg
order 5: apple, carrot
Iteration 1: Count the number of times each item occurs
item set occurrence count
{apple} 4
{egg} 3
{milk} 2
{carrot} 2
{milk} and {carrot} are eliminated because they do not meet the minimum occurrence threshold.
Iteration 2: Build item sets of size 2 using the remaining items from Iteration 1 (ie: apple, egg)
item set occurence count
{apple, egg} 3
Only {apple, egg} remains and the algorithm stops since there are no more items to add.If we had more orders and items, we can continue to iterate, building item sets consisting of more than 2 elements. For the problem we are trying to solve (ie: finding relationships between pairs of items), it suffices to implement apriori to get to item sets of size 2.
Association Rules Mining¶
Once the item sets have been generated using apriori, we can start mining association rules. Given that we are only looking at item sets of size 2, the association rules we will generate will be of the form {A} -> {B}. One common application of these rules is in the domain of recommender systems, where customers who purchased item A are recommended item B.
Here are 3 key metrics to consider when evaluating association rules:
-
support
This is the percentage of orders that contains the item set. In the example above, there are 5 orders in total and {apple,egg} occurs in 3 of them, so:support{apple,egg} = 3/5 or 60%The minimum support threshold required by apriori can be set based on knowledge of your domain. In this grocery dataset for example, since there could be thousands of distinct items and an order can contain only a small fraction of these items, setting the support threshold to 0.01% may be reasonable.
-
confidence
Given two items, A and B, confidence measures the percentage of times that item B is purchased, given that item A was purchased. This is expressed as:confidence{A->B} = support{A,B} / support{A}Confidence values range from 0 to 1, where 0 indicates that B is never purchased when A is purchased, and 1 indicates that B is always purchased whenever A is purchased. Note that the confidence measure is directional. This means that we can also compute the percentage of times that item A is purchased, given that item B was purchased:
confidence{B->A} = support{A,B} / support{B}In our example, the percentage of times that egg is purchased, given that apple was purchased is:
confidence{apple->egg} = support{apple,egg} / support{apple} = (3/5) / (4/5) = 0.75 or 75%A confidence value of 0.75 implies that out of all orders that contain apple, 75% of them also contain egg. Now, we look at the confidence measure in the opposite direction (ie: egg->apple):
confidence{egg->apple} = support{apple,egg} / support{egg} = (3/5) / (3/5) = 1 or 100%Here we see that all of the orders that contain egg also contain apple. But, does this mean that there is a relationship between these two items, or are they occurring together in the same orders simply by chance? To answer this question, we look at another measure which takes into account the popularity of both items.
-
lift
Given two items, A and B, lift indicates whether there is a relationship between A and B, or whether the two items are occuring together in the same orders simply by chance (ie: at random). Unlike the confidence metric whose value may vary depending on direction (eg: confidence{A->B} may be different from confidence{B->A}), lift has no direction. This means that the lift{A,B} is always equal to the lift{B,A}:lift{A,B} = lift{B,A} = support{A,B} / (support{A} * support{B})In our example, we compute lift as follows:
lift{apple,egg} = lift{egg,apple} = support{apple,egg} / (support{apple} * support{egg}) = (3/5) / (4/5 * 3/5) = 1.25One way to understand lift is to think of the denominator as the likelihood that A and B will appear in the same order if there was no relationship between them. In the example above, if apple occurred in 80% of the orders and egg occurred in 60% of the orders, then if there was no relationship between them, we would expect both of them to show up together in the same order 48% of the time (ie: 80% * 60%). The numerator, on the other hand, represents how often apple and egg actually appear together in the same order. In this example, that is 60% of the time. Taking the numerator and dividing it by the denominator, we get to how many more times apple and egg actually appear in the same order, compared to if there was no relationship between them (ie: that they are occurring together simply at random).
In summary, lift can take on the following values:
* lift = 1 implies no relationship between A and B. (ie: A and B occur together only by chance) * lift > 1 implies that there is a positive relationship between A and B. (ie: A and B occur together more often than random) * lift < 1 implies that there is a negative relationship between A and B. (ie: A and B occur together less often than random)In our example, apple and egg occur together 1.25 times more than random, so we conclude that there exists a positive relationship between them.
Armed with knowledge of apriori and association rules mining, let's dive into the data and code to see what relationships we unravel!
Input Dataset¶
Instacart, an online grocer, has graciously made some of their datasets accessible to the public. The order and product datasets that we will be using can be downloaded from the link below, along with the data dictionary:
“The Instacart Online Grocery Shopping Dataset 2017”, Accessed from https://www.instacart.com/datasets/grocery-shopping-2017 on September 1, 2017.
import pandas as pd
import numpy as np
import sys
from itertools import combinations, groupby
from collections import Counter
# Function that returns the size of an object in MB
def size(obj):
return "{0:.2f} MB".format(sys.getsizeof(obj) / (1000 * 1000))
Part 1: Data Preparation¶
A. Load order data¶
orders = pd.read_csv('order_products__prior.csv')
print('orders -- dimensions: {0}; size: {1}'.format(orders.shape, size(orders)))
display(orders.head())
B. Convert order data into format expected by the association rules function¶
# Convert from DataFrame to a Series, with order_id as index and item_id as value
orders = orders.set_index('order_id')['product_id'].rename('item_id')
display(orders.head(10))
type(orders)
C. Display summary statistics for order data¶
print('orders -- dimensions: {0}; size: {1}; unique_orders: {2}; unique_items: {3}'
.format(orders.shape, size(orders), len(orders.index.unique()), len(orders.value_counts())))
Part 2: Association Rules Function¶
A. Helper functions to the main association rules function¶
# Returns frequency counts for items and item pairs
def freq(iterable):
if type(iterable) == pd.core.series.Series:
return iterable.value_counts().rename("freq")
else:
return pd.Series(Counter(iterable)).rename("freq")
# Returns number of unique orders
def order_count(order_item):
return len(set(order_item.index))
# Returns generator that yields item pairs, one at a time
def get_item_pairs(order_item):
order_item = order_item.reset_index().as_matrix()
for order_id, order_object in groupby(order_item, lambda x: x[0]):
item_list = [item[1] for item in order_object]
for item_pair in combinations(item_list, 2):
yield item_pair
# Returns frequency and support associated with item
def merge_item_stats(item_pairs, item_stats):
return (item_pairs
.merge(item_stats.rename(columns={'freq': 'freqA', 'support': 'supportA'}), left_on='item_A', right_index=True)
.merge(item_stats.rename(columns={'freq': 'freqB', 'support': 'supportB'}), left_on='item_B', right_index=True))
# Returns name associated with item
def merge_item_name(rules, item_name):
columns = ['itemA','itemB','freqAB','supportAB','freqA','supportA','freqB','supportB',
'confidenceAtoB','confidenceBtoA','lift']
rules = (rules
.merge(item_name.rename(columns={'item_name': 'itemA'}), left_on='item_A', right_on='item_id')
.merge(item_name.rename(columns={'item_name': 'itemB'}), left_on='item_B', right_on='item_id'))
return rules[columns]
B. Association rules function¶
def association_rules(order_item, min_support):
print("Starting order_item: {:22d}".format(len(order_item)))
# Calculate item frequency and support
item_stats = freq(order_item).to_frame("freq")
item_stats['support'] = item_stats['freq'] / order_count(order_item) * 100
# Filter from order_item items below min support
qualifying_items = item_stats[item_stats['support'] >= min_support].index
order_item = order_item[order_item.isin(qualifying_items)]
print("Items with support >= {}: {:15d}".format(min_support, len(qualifying_items)))
print("Remaining order_item: {:21d}".format(len(order_item)))
# Filter from order_item orders with less than 2 items
order_size = freq(order_item.index)
qualifying_orders = order_size[order_size >= 2].index
order_item = order_item[order_item.index.isin(qualifying_orders)]
print("Remaining orders with 2+ items: {:11d}".format(len(qualifying_orders)))
print("Remaining order_item: {:21d}".format(len(order_item)))
# Recalculate item frequency and support
item_stats = freq(order_item).to_frame("freq")
item_stats['support'] = item_stats['freq'] / order_count(order_item) * 100
# Get item pairs generator
item_pair_gen = get_item_pairs(order_item)
# Calculate item pair frequency and support
item_pairs = freq(item_pair_gen).to_frame("freqAB")
item_pairs['supportAB'] = item_pairs['freqAB'] / len(qualifying_orders) * 100
print("Item pairs: {:31d}".format(len(item_pairs)))
# Filter from item_pairs those below min support
item_pairs = item_pairs[item_pairs['supportAB'] >= min_support]
print("Item pairs with support >= {}: {:10d}\n".format(min_support, len(item_pairs)))
# Create table of association rules and compute relevant metrics
item_pairs = item_pairs.reset_index().rename(columns={'level_0': 'item_A', 'level_1': 'item_B'})
item_pairs = merge_item_stats(item_pairs, item_stats)
item_pairs['confidenceAtoB'] = item_pairs['supportAB'] / item_pairs['supportA']
item_pairs['confidenceBtoA'] = item_pairs['supportAB'] / item_pairs['supportB']
item_pairs['lift'] = item_pairs['supportAB'] / (item_pairs['supportA'] * item_pairs['supportB'])
# Return association rules sorted by lift in descending order
return item_pairs.sort_values('lift', ascending=False)
Part 3: Association Rules Mining¶
%%time
rules = association_rules(orders, 0.01)
# Replace item ID with item name and display association rules
item_name = pd.read_csv('products.csv')
item_name = item_name.rename(columns={'product_id':'item_id', 'product_name':'item_name'})
rules_final = merge_item_name(rules, item_name).sort_values('lift', ascending=False)
display(rules_final)
Part 4: Conclusion¶
From the output above, we see that the top associations are not surprising, with one flavor of an item being purchased with another flavor from the same item family (eg: Strawberry Chia Cottage Cheese with Blueberry Acai Cottage Cheese, Chicken Cat Food with Turkey Cat Food, etc). As mentioned, one common application of association rules mining is in the domain of recommender systems. Once item pairs have been identified as having positive relationship, recommendations can be made to customers in order to increase sales. And hopefully, along the way, also introduce customers to items they never would have tried before or even imagined existed! If you wish to see the Python notebook corresponding to the code above, please click here.